不知大家在學習概率(probability) 的時候,有沒有相似的疑問:「中六合彩頭獎的機會率是½,因為是只有 “中”跟”沒中”兩個可能性。」
以上的說法很顯然是一個謬論,但概率有別於一般運算,難以證明當中的錯誤。 後來我從 Bertrand’ paradox得到一些啟發,現在藉此跟大家分享我的看法。
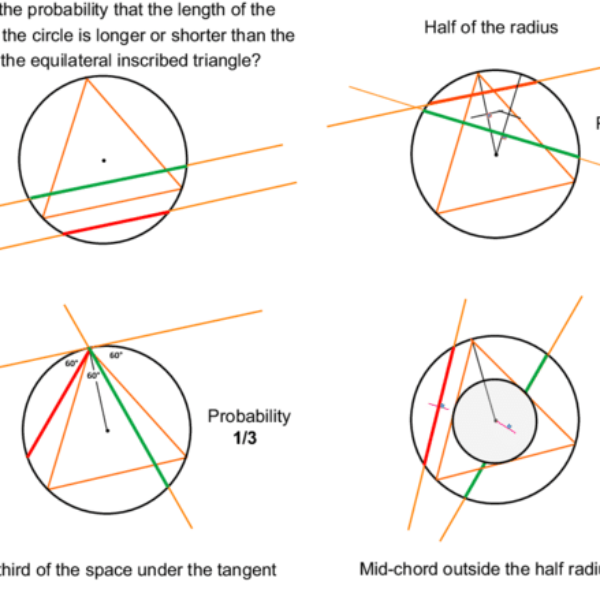
Bertrand’ paradox 的主題是探討以下的一條命題: 考慮一個內接圓的三角形,若隨機選出一條圓上的弦線,求此弦線比三角形的邊長更長的概率。 表面來看並無特別,不過Bertand 提出了3個不同的計算方法。
1. The “random endpoints” method: 全等三角形與圓形之間的空間分為3份,以三角形的頂點出發,只有穿過三角形對邊的弦線,都比三角形的邊長更長,得到的概率將是⅓。

2. The “random radial point” method: 以半徑作為弦線的中點作考慮,任何處於圓心和三角形邊長之間的弦線,都比三角形的邊長更長,得到的概率將是½。

3. The “random midpoint” method: 考慮三角形的內接圓,任何穿過內接圓的弘線,都比三角形的邊長更長,得到的概率將是¼。

Bertrand’ paradox 的目的非在於解釋哪個是錯誤的方法,而且以上的計算都沒有錯誤。 歸根究底,會形成這個矛盾的原因,其中之一就是三種方法各自根據不同的「公平原則」來分割圖形,自然會有不同的結論。因此,單憑 “中”跟”沒中”粗略計算中獎的可能性,兩件事件本身並不對等,自然不應該得到½ 這個結論。
